Find the Solution to a Sequence
By Paul Reiners
Published March 11, 2008
Genetics databases hold extremely large amounts of raw data. The human genome alone has approximately 3 billion DNA base pairs. To search through all this data and find meaningful relationships within it, molecular biologists are depending more and more on efficient computer science string algorithms. This article introduces you to three such algorithms, all of which use dynamic programming, an advanced algorithmic technique that solves optimization problems from the bottom up by finding optimal solutions to subproblems. You'll work through Java™ implementations of these algorithms, and you'll learn about an open source Java framework for processing biological data.
Genetics and string algorithms
Strands of genetic material — DNA and RNA — are sequences of small units called nucleotides. For purposes of answering some important research questions, genetic strings are equivalent to computer science strings — that is, they can be thought of as simply sequences of characters, ignoring their physical and chemical properties. (Although, strictly speaking, their chemical properties are usually coded as parameters to the string algorithms you'll be looking at in this article.)
This article's examples use DNA, which consists of two strands of adenine (A), cytosine (C), thymine (T), and guanine (G) nucleotides. DNA's two strands are reverse complements of each other. A and T are complementary bases, and C and G are complementary bases. This means that A s in one strand are paired with T s in the other strand (and vice versa), and C s in one strand are paired with G s in the other strand (and vice versa). So, if you know the sequence of one strand's A s, C s, T s, and G s, you can derive the other strand's sequence. Hence, you can think of a DNA strand simply as a string of the letters A, C, G, and T.
Dynamic programming
Dynamic programming is an algorithmic technique used commonly in sequence analysis. Dynamic programming is used when recursion could be used but would be inefficient because it would repeatedly solve the same subproblems. For example, consider the Fibonacci sequence: 0, 1, 1, 2, 3, 5, 8, 13, … The first and second Fibonacci numbers are defined to be 0 and 1, respectively. The _n_th Fibonacci number is defined to be the sum of the two preceding Fibonacci numbers. So, you can calculate the _n_th Fibonacci number with the recursive function in Listing 1:
Listing 1. Recursive function for calculating nth Fibonacci number
public int fibonacci1(int n) { if (n == 0) { return 0; } else if (n == 1) { return 1; } else { return fibonacci1(n ‑ 1) + fibonacci1(n ‑ 2); } } But Listing 1's code is inefficient because it solves some of the same recursive subproblems repeatedly. For example, consider the computation of fibonacci1(5), represented in Figure 1:
Figure 1. Recursive computation of Fibonacci numbers
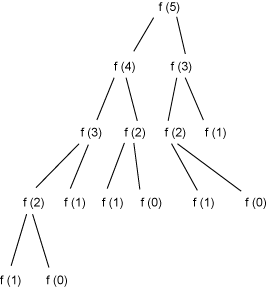
In Figure 1 you can see, for example, that fibonacci1(2) is computed three times. It would be much more efficient to build the Fibonacci numbers from the bottom up, as shown in Listing 2, rather than from the top down:
Listing 2. Building Fibonacci numbers from the bottom up
public int fibonacci2(int n) { int[] table = new int[n + 1]; for (int i = 0; i < table.length; i++) { if (i == 0) { table[i] = 0; } else if (i == 1) { table[i] = 1; } else { table[i] = table[i ‑ 2] + table[i ‑ 1]; } } return table[n]; } Listing 2 stores the intermediate results in a table so that you can reuse them, rather than throwing them away and computing them multiple times. It's true that storing the table is memory-inefficient because you use only two entries of the table at a time, but ignore that fact for now. I'm doing it this way to motivate your use of similar tables (although they will be two-dimensional) in this article's more complicated later examples. The point is that Listing 2's implementation is much more time-efficient than Listing 1's. Listing 2's implementation runs in O(n) time. I won't prove this, but the running time of Listing 1's naive, recursive implementation is exponential in n.
This is exactly how dynamic programming works. You take a problem that could be solved recursively from the top down and solve it iteratively from the bottom up instead. You store your intermediate results in a table for later use; otherwise, you would end up computing them repeatedly — an inefficient algorithm. But dynamic programming is usually applied to optimization problems like the rest of this article's examples, rather than to problems like the Fibonacci problem. The next example is a string algorithm, like those commonly used in computational biology.
Longest common subsequence problem
You'll first see how to use dynamic programming to find a longest common subsequence (LCS) of two DNA sequences. Biologists who find a new gene sequence typically want to know what other sequences it is most similar to. Finding an LCS is one way of computing how similar two sequences are: the longer the LCS is, the more similar they are.
The characters in a subsequence, unlike those in a substring, do not need to be contiguous. For example, ACE is a subsequence (but not a substring) of ABCDE. Consider the following two DNA sequences:
- S1 =
GCCCTAGCG - S2 =
GCGCAATG
It turns out that an LCS of these two sequences is GCCAG. (Note that this is an LCS, rather than the LCS, because other common subsequences of the same length might exist. This and the other optimization problems you'll look at might have more than one solution.)
LCS algorithm
First, think about how you might compute an LCS recursively. Let:
- C1 be the right-most character of S1
- C2 be the right-most character of S2
- S1′ be S1 with C1 "chopped-off"
- S2′ be S2 with C2 "chopped-off"
There are three recursive subproblems:
- L1 = LCS(S1′, S2)
- L2 = LCS(S1, S2′)
- L3 = LCS(S1′, S2′)
I won't prove this, but it can be shown (and it's not hard to believe) that the solution to the original problem is whichever of these is the longest:
- L1
- L2
- L3 appended with C1 if C1 equals C2, or L3 if C1 is not equal to C2
(The base case is whenever S1 or S2 is a zero-length string. In this case, the LCS of S1 and S2 is clearly a zero-length string.)
However, like the recursive procedure for computing Fibonacci numbers, this recursive solution requires multiple computations of the same subproblems. It can be shown that this recursive solution takes exponential time to run. In contrast, the dynamic programming solution to this problem runs in Θ(mn) time, where m and n are the lengths of the two sequences.
To compute the LCS efficiently using dynamic programming, you start by constructing a table in which you build up partial results. List one of the sequences across the top and the other down the left, as shown in Figure 2:
Figure 2. Initial LCS table
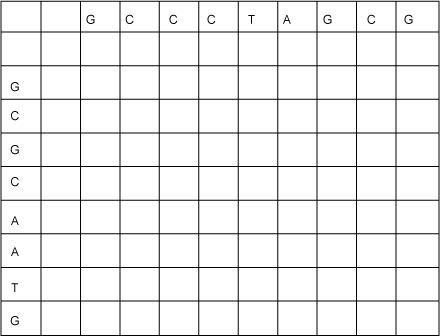
The idea is that you'll fill up the table from top to bottom, and from left to right, and each cell will contain a number that is the length of an LCS of the two string prefixes up to that row and column. That is, each cell will contain a solution to a subproblem of the original problem. For example, consider the cell in the sixth row and the seventh column; it is to the right of the second C in GCGCAATG and below the T in GCCCTAGCG. This cell will eventually contain a number that is the length of an LCS of GCGC and GCCCT.
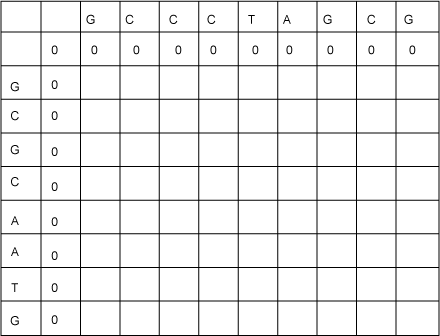
First consider what the entries should be for the table's second row. These are the lengths of LCSs for the zero-length prefix of the sequence going down the left, GCGCAATG, and prefixes of the sequence along the top, GCCCTAGCG. Clearly, the value of any of these LCSs will be 0. Similarly, the values down the second columns will all be 0. This corresponds to the base case of the recursive solution. Now the table looks like Figure 3:
Figure 3. LCS table with base cases filled in
Next, you implement what corresponds to the recursive subcases in the recursive algorithm, but you use values that you've already filled in. In Figure 4, I've filled in about half of the cells:
Figure 4. LCS table half filled-in
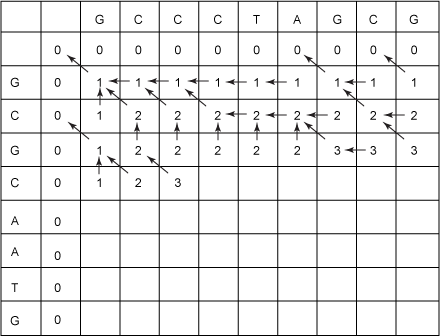
When you fill in a cell, you consider:
- The cell directly to the left of it
- The cell directly above it
- The cell to the above-left of it
The three values below correspond, respectively, to the values returned by the three recursive subproblems I listed earlier.
- V1 = the value in the cell to the left
- V2 = the value in the cell above
- V3 = the value in the cell to the above-left
You fill in the empty cell with the maximum of these three numbers:
- V1
- V2
- V3 + 1 if C1 equals C2, or V3 if C1 is not equal to C2, where C1 is the character above the current cell and C2 is the character to the left of the current cell
Note that I also add arrows that point back to which of those three cells I used to get the value for the current cell. You'll use these arrows later in "tracing back" to construct an actual LCS (as opposed to just discovering the length of one).
Now fill in the next blank cell in Figure 4 — the one under the third C in GCCCTAGCG and to the right of the second C in GCGCAATG. You have a 2 above it, a 3 to the left of it, and a 2 to the above-left of it. The character above this cell and the character to the left of this cell are equal (they're both C), so you must pick the maximum of 2, 3, and 3 (2 from the above-left cell + 1). So, the value of this cell will be 3. Draw an arrow back to the cell from which you got this new number. In this case, where the new number could have come from more than one cell, pick an arbitrary one: the one to the above-left, say.
As an exercise, you might want to try filling in the rest of the table. If, in the case of ties, you always choose the cell to the above-left over the cell above and the cell above over the cell to the left, you'll get the table in Figure 5. (If you make different choices in the case of ties, your arrows will be different, of course, but the numbers will be the same.)
Figure 5. Filled-in LCS table
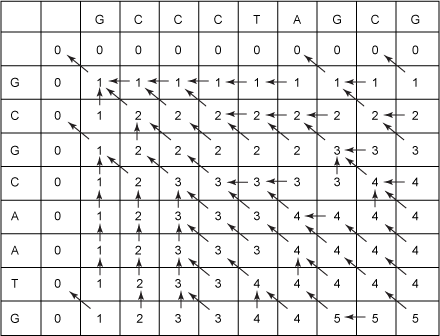
Recall that the number in any cell is the length of an LCS of the string prefixes above and below that end in the column and row of that cell. Hence, the number in the lower, right-most cell is the length of an LCS of the two strings S1 and S2— GCCCTAGCG and GCGCAATG in this case. So, the length of an LCS for these two sequences is 5.
This is a key point to keep in mind with all of these dynamic programming algorithms. Each cell in the table contains the solution to the problem for the sequence prefixes above and to the left that end at the column and row of that cell.
Tracing back to find an actual LCS
The next thing you want to do is to find an actual LCS. You do this in the traceback step in which you use the cell pointers that you drew. When you're building up your table, remember that when you have a pointer to the above-left cell, and the value in the current cell is 1 more than the value of the above-left cell, this means that the characters to the left and above are equal. In building up an LCS, this corresponds to adding this character to the LCS. So, the way you construct an LCS is by starting in the lower-right corner cell and then following the pointer arrows backward. Every time you follow a pointer to a diagonal cell to the above-left and the value of the cell that is pointed to is 1 less than the value of the current cell, you prepend the corresponding common character to the LCS you're constructing. Note that you prepend it because you're starting at the end of the LCS. (In the case of Figure 5, the 5 in the lower-right cell corresponds to the fifth character you've added.)
So, proceed to build up your LCS. Starting in the lower-right cell, you see that you have the cell pointer pointing to the above-left and that the value in the current cell (5) is one more than the value in the cell to the above-left (4). So you prepend the character G to your initial zero-length string. The next arrow, from the cell containing a 4, also points up and to the left, but the value doesn't change. And the next cell also points to the left and above, but its value also doesn't change. Finally, that cell also points to the above and left, but the value went from 3 to 4. This means you added the common character in that row and column, which is an A. So, your LCS so far is AG. From there, you follow the pointer to the left (this corresponds to skipping over the T above) to another 3. Then there is a diagonal pointer pointing to a 2. Hence, you add the common letter in the current row and column, which is a C, yielding CAG. You continue in this fashion until you finally reach a 0. Figure 6 shows the entire traceback:
Figure 6. Filled-in LCS table with traceback
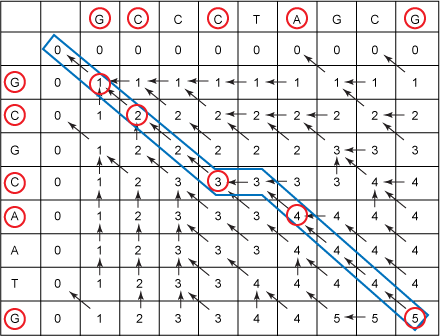
From the traceback, you get GCCAG as an LCS.
Dynamic programming implementation in the Java language
Now you'll use the Java language to implement dynamic programming algorithms — the LCS algorithm first and, a bit later, two others for performing sequence alignment. In each example you'll somehow compare two sequences, and you'll use a two-dimensional table to store the solutions to subproblems. You'll define an abstract DynamicProgramming class that contains code common to all the algorithms. All of this article's sample code is available for Download.
To start, you need a class representing cells in the table, as shown in Listing 3:
Listing 3. Cell class (partial listing)
public class Cell { private Cell prevCell; private int score; private int row; private int col; } The first step in all the algorithms is to initialize the scores and sometimes the pointers in the table. What you set the initial scores and pointers to differs from algorithm to algorithm, which is why the DynamicProgramming class, as shown in Listing 4, defines two abstract methods:
Listing 4. DynamicProgramming initialization code
protected void initialize() { for (int i = 0; i < scoreTable.length; i++) { for (int j = 0; j < scoreTable[i].length; j++) { scoreTable[i][j] = new Cell(i, j); } } initializeScores(); initializePointers(); isInitialized = true; } protected void initializeScores() { for (int i = 0; i < scoreTable.length; i++) { for (int j = 0; j < scoreTable[i].length; j++) { scoreTable[i][j].setScore(getInitialScore(i, j)); } } } protected void initializePointers() { for (int i = 0; i < scoreTable.length; i++) { for (int j = 0; j < scoreTable[i].length; j++) { scoreTable[i][j].setPrevCell(getInitialPointer(i, j)); } } } protected abstract int getInitialScore(int row, int col); protected abstract Cell getInitialPointer(int row, int col); Next, you fill in each cell of the table with a score and a pointer. Again, how you do this varies from algorithm to algorithm, so you use an abstract method, fillInCell(Cell, Cell, Cell, Cell). Listing 5 shows DynamicProgramming's methods for filling in the table:
Listing 5. DynamicProgramming code for filling in the table
protected void fillIn() { for (int row = 1; row < scoreTable.length; row++) { for (int col = 1; col < scoreTable[row].length; col++) { Cell currentCell = scoreTable[row][col]; Cell cellAbove = scoreTable[row ‑ 1][col]; Cell cellToLeft = scoreTable[row][col ‑ 1]; Cell cellAboveLeft = scoreTable[row ‑ 1][col ‑ 1]; fillInCell(currentCell, cellAbove, cellToLeft, cellAboveLeft); } } } protected abstract void fillInCell(Cell currentCell, Cell cellAbove, Cell cellToLeft, Cell cellAboveLeft); Finally, you get the traceback. How you do this varies across algorithms. Listing 6 shows the DynamicProgramming.getTraceback() method:
Listing 6. DynamicProgramming.getTraceback() method
abstract protected Object getTraceback(); Java LCS implementation
Now, you're ready to code a Java implementation for the LCS algorithm.
Initializing the scores in the cells is easy: you just set them all initially to 0 (you'll reset some of them later), as shown in Listing 7:
Listing 7. LCS initialization method
protected int getInitialScore(int row, int col) { return 0; } Listing 8 shows the code for filling in the score and pointer for an individual cell in the table:
Listing 8. LCS method for filling in a cell's score and pointer
protected void fillInCell(Cell currentCell, Cell cellAbove, Cell cellToLeft, Cell cellAboveLeft) { int aboveScore = cellAbove.getScore(); int leftScore = cellToLeft.getScore(); int matchScore; if (sequence1.charAt(currentCell.getCol() ‑ 1) == sequence2 .charAt(currentCell.getRow() ‑ 1)) { matchScore = cellAboveLeft.getScore() + 1; } else { matchScore = cellAboveLeft.getScore(); } int cellScore; Cell cellPointer; if (matchScore >= aboveScore) { if (matchScore >= leftScore) { // matchScore >= aboveScore and matchScore >= leftScore cellScore = matchScore; cellPointer = cellAboveLeft; } else { // leftScore > matchScore >= aboveScore cellScore = leftScore; cellPointer = cellToLeft; } } else { if (aboveScore >= leftScore) { // aboveScore > matchScore and aboveScore >= leftScore cellScore = aboveScore; cellPointer = cellAbove; } else { // leftScore > aboveScore > matchScore cellScore = leftScore; cellPointer = cellToLeft; } } currentCell.setScore(cellScore); currentCell.setPrevCell(cellPointer); } Finally, you construct an actual LCS using the traceback:
Listing 9. LCS traceback code
protected Object getTraceback() { StringBuffer lCSBuf = new StringBuffer(); Cell currentCell = scoreTable[scoreTable.length ‑ 1][scoreTable[0].length ‑ 1]; while (currentCell.getScore() > 0) { Cell prevCell = currentCell.getPrevCell(); if ((currentCell.getRow() ‑ prevCell.getRow() == 1 && currentCell .getCol() ‑ prevCell.getCol() == 1) && currentCell.getScore() == prevCell.getScore() + 1) { lCSBuf.insert(0, sequence1.charAt(currentCell.getCol() ‑ 1)); } currentCell = prevCell; } return lCSBuf.toString(); } It's pretty easy to see that this algorithm takes Θ(mn) time (and space) to compute, where m and n are the lengths of the two sequences. Filling in each cell takes constant time — just a bounded number of additions and comparisons — and you must fill in mn cells. Also, the traceback runs in O(m + n) time.
The next two Java examples implement-sequence alignment algorithms: Needleman-Wunsch and Smith-Waterman.
Sequence alignment
Homology
Homology is an important biological concept. Two species are considered homologous if they share a common evolutionary ancestor. Homologous species have many parts of their DNA in common. Conversely, if two species have a similar substring of DNA, you can often infer that this similar DNA comes from a common ancestor. Sequence-alignment algorithms can be used to find such similar DNA substrings.
A major theme of genomics is comparing DNA sequences and trying to align the common parts of two sequences. If two DNA sequences have similar subsequences in common — more than you would expect by chance — then there is a good chance that the sequences are homologous (see " Homology" sidebar). In aligning two sequences, you consider not only characters that match identically, but also spaces or gaps in one sequence (or, conversely, insertions in the other sequence) and mismatches, both of which can correspond to mutations. In sequence alignment, you want to find an optimal alignment that, loosely speaking, maximizes the number of matches and minimizes the number of spaces and mismatches. More formally, you can determine a score for each possible alignment by adding points for matching characters and subtracting points for spaces and mismatches.
Global and local sequence alignment
Global sequence alignment tries to find the best alignment between an entire sequence S1 and another entire sequence S2. Consider these two DNA sequences:
- S1 =
GCCCTAGCG - S2 =
GCGCAATG
If you award matches one point, penalize spaces by two points, and penalize mismatches by one point, the following is an optimal global alignment:
- S1′ =
GCCCTAGCG - S2′ =
GCGC-AATG
A dash (-) denotes a space. There are five matches, one space in S2′ (or, conversely, one insertion in S1′), and three mismatches. This yields a score of (5 1) + (1 -2) + (3 * -1) = 0, which is the best you can do.
With local sequence alignment, you're not constrained to aligning the whole of both sequences; you can just use parts of each to obtain a maximum score. Using the same sequences S1 and S2 and the same scoring scheme, you obtain the following optimal local alignment S1" and S2":
- S1 = GCCCTAGCG
S1= GCCCTAGCG - S1" = GCG
S1'' = GCG - S2" = GCG
S2'' = GCG - S2 = GCGCAATG
S2= GCGCAATG
This local alignment doesn't happen to have any mismatches or spaces, although, in general, local alignments can have them. This local alignment has a score of (3 1) + (0 -2) + (0 * -1) = 3. (The score of the best local alignment is greater than or equal to the score of the best global alignment, because a global alignment is a local alignment.)
Needleman-Wunsch algorithm
The Needleman-Wunsch algorithm is used for computing global alignments. The idea is similar to the LCS algorithm. Again, you have a two-dimensional table with one sequence along the top and one along the left side. Again, you can arrive at each cell in one of three ways:
- From the cell above, which corresponds to aligning the character to the left with a space
- From the cell to the left, which corresponds to aligning the character above with a space
- From the cell diagonally to the above-left, which corresponds to aligning the characters to the left and above (which might or might not match)
I'll first give you the whole table (see Figure 7), and you can refer back to it as I explain how it was filled in:
Figure 7. Filled-in Needleman-Wunsch table with traceback
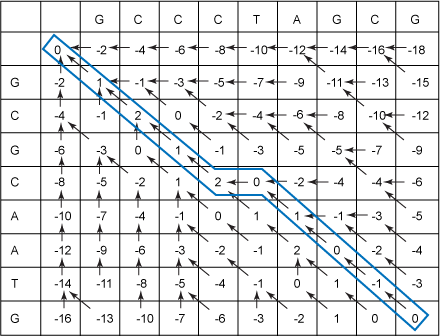
First, you must initialize the table. This means filling in the scores and pointers for the second row and second column. Traveling to the right in the second row corresponds to using a character in the first sequence along the top and using a space, rather than the first character of the sequence going down the left. The space penalty is -2, so, each time you do this, you add -2 to the previous cell. The previous cell is the one to the left. So, this explains how you get the 0, -2, -4, -6, … sequence in the second row. Similarly, you obtain the scores and pointers going down the second column. Listing 10 shows initialization code for the Needleman-Wunsch algorithm:
Listing 10. Needleman-Wunsch initialization code
protected Cell getInitialPointer(int row, int col) { if (row == 0 && col != 0) { return scoreTable[row][col ‑ 1]; } else if (col == 0 && row != 0) { return scoreTable[row ‑ 1][col]; } else { return null; } } protected int getInitialScore(int row, int col) { if (row == 0 && col != 0) { return col ∗ space; } else if (col == 0 && row != 0) { return row ∗ space; } else { return 0; } } Next, you need to fill in the remaining cells. As with the LCS algorithm, for each cell you have three choices and pick the maximum one. You can come at each cell from above, from the left, or from the above-left. Let S1 and S2 be the strings you're trying to align, and S1′ and S2′ be the strings in the resulting alignment. Coming at the cell from above is the same as adding the character at the left from S2 to S2′, while skipping the character in S1 above for now and introducing a space in S1′. Because a space has a score of -2, you would obtain a score for the current cell by subtracting 2 from the cell above. Similarly, you could come to the blank cell from the left by subtracting 2 from the score in the cell to the left. Finally, you could add the character above to S1′ and the character to the left to S2′. This corresponds to entering the blank cell from the above-left. These two characters will match, in which case the new score is the score in the cell to the above-left plus 1; or they won't match, in which case the new score is the score in the cell to the above-left minus 1. Of these three possibilities, you pick one that gives you the maximum score (picking an arbitrary high-scoring cell, if there is a tie). If you look at the pointers in Figure 7, you can find examples of each of these three possibilities.
Listing 11 shows the code for filling in the blank cells:
Listing 11. Needleman-Wunsch code for filling in the table
protected void fillInCell(Cell currentCell, Cell cellAbove, Cell cellToLeft, Cell cellAboveLeft) { int rowSpaceScore = cellAbove.getScore() + space; int colSpaceScore = cellToLeft.getScore() + space; int matchOrMismatchScore = cellAboveLeft.getScore(); if (sequence2.charAt(currentCell.getRow() ‑ 1) == sequence1 .charAt(currentCell.getCol() ‑ 1)) { matchOrMismatchScore += match; } else { matchOrMismatchScore += mismatch; } if (rowSpaceScore >= colSpaceScore) { if (matchOrMismatchScore >= rowSpaceScore) { currentCell.setScore(matchOrMismatchScore); currentCell.setPrevCell(cellAboveLeft); } else { currentCell.setScore(rowSpaceScore); currentCell.setPrevCell(cellAbove); } } else { if (matchOrMismatchScore >= colSpaceScore) { currentCell.setScore(matchOrMismatchScore); currentCell.setPrevCell(cellAboveLeft); } else { currentCell.setScore(colSpaceScore); currentCell.setPrevCell(cellToLeft); } } } Next, you need to obtain the actual alignment strings —S1′ and S2′— and the alignment score. The score in the bottom-right cell contains the maximum alignment score for S1 and S2, just as it contains the length of an LCS in the LCS algorithm. And, similarly to the LCS algorithm, to obtain S1′ and S2′, you trace back from this bottom-right cell, following the pointers, and build up S1′ and S2′ in reverse. From constructing the table, you know that going down corresponds to adding the character to the left from S2 to S2′ while adding a space to S1′; going right corresponds to adding the character above from S1 to S1′ while adding a space to S2′; and going down and to the right means adding a character from S1 and S2 to S1′ and S2′, respectively.
The traceback code that you use for Needleman-Wunsch turns out to be identical to that used for Smith-Waterman for local alignment, except for determining which cell you start in and how you know when to finish the traceback. Listing 12 shows the code that the two algorithms share:
Listing 12. Traceback code used for both Needleman-Wunsch and Smith-Waterman
protected Object getTraceback() { StringBuffer align1Buf = new StringBuffer(); StringBuffer align2Buf = new StringBuffer(); Cell currentCell = getTracebackStartingCell(); while (traceBackIsNotDone(currentCell)) { if (currentCell.getRow() ‑ currentCell.getPrevCell().getRow() == 1) { align2Buf.insert(0, sequence2.charAt(currentCell.getRow() ‑ 1)); } else { align2Buf.insert(0, '‑'); } if (currentCell.getCol() ‑ currentCell.getPrevCell().getCol() == 1) { align1Buf.insert(0, sequence1.charAt(currentCell.getCol() ‑ 1)); } else { align1Buf.insert(0, '‑'); } currentCell = currentCell.getPrevCell(); } String[] alignments = new String[] { align1Buf.toString(), align2Buf.toString() }; return alignments; } protected abstract boolean traceBackIsNotDone(Cell currentCell); protected abstract Cell getTracebackStartingCell(); Listing 13 shows the traceback code specific to Needleman-Wunsch:
Listing 13. Needleman-Wunsch traceback code
protected boolean traceBackIsNotDone(Cell currentCell) { return currentCell.getPrevCell() != null; } protected Cell getTracebackStartingCell() { return scoreTable[scoreTable.length ‑ 1][scoreTable[0].length ‑ 1]; } The original Needleman-Wunsch algorithm
Strictly speaking, I haven't shown you the Needleman-Wunsch algorithm. The original algorithm published by Needleman-Wunsch runs in cubic time and is no longer used. However, the quadratic algorithm discussed here is still commonly referred to as the Needleman-Wunsch algorithm.
Tracing backwards gives you the optimal global alignment I mentioned at the beginning of this section:
- S1′ =
GCCCTAGCG - S2′ =
GCGC-AATG
Clearly, this algorithm runs in O(mn) time.
Smith-Waterman algorithm
In the Smith-Waterman algorithm, you're not constrained to aligning the entire sequences. This, and the fact that two zero-length strings is a local alignment with score of 0, means that in building up a local alignment you don't need to "go into the red" and have partial scores that are negative. That would cause further alignments to have a score lower than you could get by "resetting" with two zero-length strings. Also, your local alignment doesn't need to end at the end of either sequence, so you don't need to start your traceback in the bottom-right corner; you can start it in the cell with the highest score.
This leads to three ways that the Smith-Waterman algorithm differs from the Needleman-Wunsch algorithm. First, in the initialization stage, the first row and first column are all filled in with 0s (and the pointers in the first row and first column are all null). Listing 14 shows the Smith-Waterman initialization code:
Listing 14. Smith-Waterman initialization
protected int getInitialScore(int row, int col) { return 0; } protected Cell getInitialPointer(int row, int col) { return null; } Second, when you fill in the table, if a score becomes negative, you put in 0 instead, and you add the pointer back only for cells that have positive scores. Note in Listing 15 that you also keep track of which cell has the high score; you'll need that for the traceback:
Listing 15. Smith-Waterman code for filling in a cell
protected void fillInCell(Cell currentCell, Cell cellAbove, Cell cellToLeft, Cell cellAboveLeft) { int rowSpaceScore = cellAbove.getScore() + space; int colSpaceScore = cellToLeft.getScore() + space; int matchOrMismatchScore = cellAboveLeft.getScore(); if (sequence2.charAt(currentCell.getRow() ‑ 1) == sequence1 .charAt(currentCell.getCol() ‑ 1)) { matchOrMismatchScore += match; } else { matchOrMismatchScore += mismatch; } if (rowSpaceScore >= colSpaceScore) { if (matchOrMismatchScore >= rowSpaceScore) { if (matchOrMismatchScore > 0) { currentCell.setScore(matchOrMismatchScore); currentCell.setPrevCell(cellAboveLeft); } } else { if (rowSpaceScore > 0) { currentCell.setScore(rowSpaceScore); currentCell.setPrevCell(cellAbove); } } } else { if (matchOrMismatchScore >= colSpaceScore) { if (matchOrMismatchScore > 0) { currentCell.setScore(matchOrMismatchScore); currentCell.setPrevCell(cellAboveLeft); } } else { if (colSpaceScore > 0) { currentCell.setScore(colSpaceScore); currentCell.setPrevCell(cellToLeft); } } } if (currentCell.getScore() > highScoreCell.getScore()) { highScoreCell = currentCell; } } Finally, in the traceback, you start with the cell that has the highest score and work back until you reach a cell with a score of 0. Otherwise, the traceback works exactly the same as in the Needleman-Wunsch algorithm. Listing 16 shows the Smith-Waterman traceback code:
Listing 16. Smith-Waterman traceback code
protected boolean traceBackIsNotDone(Cell currentCell) { return currentCell.getScore() != 0; } protected Cell getTracebackStartingCell() { return highScoreCell; } Figure 8 illustrates running the Smith-Waterman algorithm on the S1 and S2 sequences that you've been using throughout this article:
Figure 8. Filled-in Smith-Waterman table with traceback
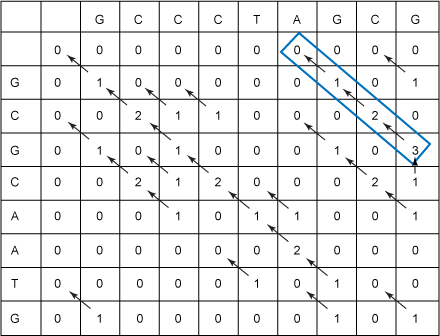
As with the Needleman-Wunsch algorithm, the optimal local alignment that you get from running the Smith-Waterman code (or from reading from Figure 8) is:
- S1 = GCCCTAGCG
S1= GCCCTAGCG - S1" = GCG
S1'' = GCG - S2" = GCG
S2'' = GCG - S2 = GCGCAATG
S2= GCGCAATG
ALIGN, FASTA, and BLAST
This article shows you basic implementations of the Needleman-Wunsch and Smith-Waterman algorithms, without optimizations, for finding global and local alignments in O(mn) time. Real-world researchers are usually not comparing two sequences, but are instead trying to find all sequences similar to a particular sequence. If one of the similar sequences they find has a known biological function, then there is a good chance that the original sequence has a similar function because similar sequences are likely to have similar functions. ALIGN, FASTA, and BLAST (Basic Local Alignment Search Tool) are industrial-grade applications that find global (ALIGN) and local (FASTA and BLAST) alignments. BLAST searches large sequence databases for sequences that are similar (and possibly homologous) to a user-input sequence and ranks the results by similarity. BLAST doesn't use Smith-Waterman directly because, even with a quadratic running time, it would be too slow at comparing a sequence against each sequence in extremely large databases of gene sequences, each of which may consist of as many as 3 billion base pairs (or more). Instead, BLAST first uses a process called seeding to find seeds, which are the beginnings of possible matches or hits. BLAST then uses a dynamic programming algorithm to extend the possible hits found to actual local alignments with the input sequence. Finally, it finds which of the matches are statistically significant and ranks them. This partly heuristic process isn't as sensitive (accurate) as Smith-Waterman, but it's much quicker.
BioJava
BioJava is an open source project developing a Java framework for processing biological data. Its features include objects for manipulating biological sequences, tools for making sequence-analysis GUIs, and analysis and statistical routines that include a dynamic-programming toolkit.
Listing 17 shows how to run the BioJava implementations of Needleman-Wunsch and Smith-Waterman on the same sequences and scoring scheme this article's earlier examples use:
Listing 17. BioJava code sequence alignment code (based on BioJava example code by Andreas Dräger)
// The alphabet of the sequences. For this example DNA is chosen. FiniteAlphabet alphabet = (FiniteAlphabet) AlphabetManager .alphabetForName("DNA"); // Use a substitution matrix with equal scores for every match and every // replace. int match = 1; int replace = ‑1; SubstitutionMatrix matrix = new SubstitutionMatrix(alphabet, match, replace); // Firstly, define the expenses (penalties) for every single operation. int insert = 2; int delete = 2; int gapExtend = 2; // Global alignment. SequenceAlignment aligner = new NeedlemanWunsch(match, replace, insert, delete, gapExtend, matrix); Sequence query = DNATools.createDNASequence("GCCCTAGCG", "query"); Sequence target = DNATools.createDNASequence("GCGCAATG", "target"); // Perform an alignment and save the results. aligner.pairwiseAlignment(query, // first sequence target // second one ); // Print the alignment to the screen System.out.println("Global alignment with Needleman‑Wunsch:\n" + aligner.getAlignmentString()); // Perform a local alignment from the sequences with Smith‑Waterman. aligner = new SmithWaterman(match, replace, insert, delete, gapExtend, matrix); // Perform the local alignment. aligner.pairwiseAlignment(query, target); System.out.println("\nLocal alignment with Smith‑Waterman:\n" + aligner.getAlignmentString()); The BioJava methods have a little more generality to them. First, note the use of a SubstitutionMatrix. The examples so far have naively assumed that the penalty for a mismatch between DNA bases should be equal — for example, that a G is as likely to mutate into an A as a C. But this isn't true in real biological sequences, especially amino acids in proteins. You want to penalize unlikely mismatches more than likely mismatches. A substitution matrix lets you assign match scores individually to each pair of symbols. In a sense, substitution matrices code up chemical properties. For example, the BLOSUM (BLOcks SUbstitution Matrix) matrices for proteins are commonly used in BLAST searches; the values in the BLOSUM matrices were empirically determined.
Next, note the use of insert and delete scores, rather than just a single space score. As I've said, you can think of a space as an insertion in the sequence without the space, or as a deletion in the sequence with the space. In general, there are two complementary ways to compare two sequences. You've been looking at them in a "static" manner and seeing how they differ. You can also compare them by finding the minimum number of insertions, deletions, and changes of individual symbols you'd have to make to one sequence to transform it into the other. This minimum number of changes is called the edit distance. When calculating the edit distance, you might want to assign different values to insertions and deletions. For example, maybe insertions are more common and you'd want to penalize them less than deletions.
Use of Perl in bioinformatics
Much of the big-server bioinformatics software is written in C or C . BLAST was originally written in C, and now there's a C version. But many of the small applications written by researchers — who, in many cases, might be professional biologists first and programmers a distant second — are written in Perl. This could be because the biggest open source bioinformatics library, Bioperl, is written in Perl. If you want to get a job doing bioinformatics programming, you'll probably need to learn Perl and Bioperl at some point.
Now note the gapExtend variable. Technically, a gap is a maximal sequence of contiguous spaces. However, some of the literature uses the term gap when it really means a space. You've scored all spaces equally even when they're part of a larger gap. However, in nature, once a gap has started, the chance of it extending by another space is greater than the chance of it starting to begin with. So, to get meaningful results, you would want to penalize subsequent spaces in a gap less than the initial space in the gap. This is what the gapExtend variable is for. Keep in mind that, algorithmically speaking, all these scoring schemes are somewhat arbitrary, but obviously you want the string edit distances you're computing to conform to evolutionary distances in nature as closely as possible. (Coming up with appropriate scoring schemes for different situations is quite an interesting and complicated subfield in itself.)
Finally, the insert, delete, and gapExtend variables have positive values, rather than the negative values you used earlier because they are defined as expenses (costs or penalties).
When you run the code in Listing 17, you get the following output:
Listing 18. Output
Global alignment with Needleman‑Wunsch: Length:9 Score:‑0.0 Query:query,Length:9 Target:target,Length:8 Query: 1 gccctagcg 9 || | | | Target: 1 gcgc‑aatg 8 Local alignment with Smith‑Waterman: Length:3 Score:3.0 Query:query,Length:9 Target:target,Length:8 Query: 7 gcg 9 ||| Target: 1 gcg 3 For both local and global alignment, you get the same scores as you did earlier. This implementation of Smith-Waterman gives you the same local alignment you obtained earlier. This implementation of Needleman-Wunsch gives you a different global alignment, but with the same score, from the one you obtained earlier. However, they're both maximal global alignments. Recall that when you're filling out your table, you can sometimes get a maximum score in a cell from more than one of the previous cells. Depending on which one you choose to point back to, you will end up with different alignments (but all with the same score).
Conclusion
This article has looked at three examples of problems that can be solved using dynamic programming. They all share these characteristics:
- The solution to each of them could be expressed as a recurrence relation.
- The naive implementation of this recurrence relation as a recursive method would have led to an inefficient solution involving multiple computations of subproblems.
- An optimal solution to the problem could be constructed from optimal solutions to subproblems of the original problem.
Dynamic programming is also used in matrix-chain multiplication, assembly-line scheduling, and computer chess programs. It's often needed to solve tough problems in programming contests. Interested readers can consult the book Introduction to Algorithms for more details on when dynamic programming is applicable and how the correctness of dynamic programming algorithms is usually proved.
Dynamic programming is maybe the most important use of computer science in biology, but certainly not the only one. Bioinformatics and computational biology are interdisciplinary fields that are quickly becoming disciplines in themselves with academic programs dedicated to them. Many molecular biologists now know a little programming, and there's much interesting and important work to be done by programmers who can learn a little biology.
Acknowledgments
Thanks to Sonna Bristle, who got me interested in computational biology, and Carlos P. Sosa of IBM for reviewing a version of this article and giving helpful suggestions.
Find the Solution to a Sequence
Source: https://developer.ibm.com/articles/j-seqalign/